Matrix multiplication on RISC-V low-power processor
In collaboration with Jie Lei and under supervision of Enrique Quintana y Adrián Castelló.
Full Text
@article{ramirez2022blis,
title={A BLIS-like matrix multiplication for machine learning in the RISC-V ISA-based GAP8 processor},
author={Ramírez, Cristian and Castellón, Adrián and Quintana-Ortí, Enrique S},
journal={The Journal of Supercomputing},
pages={1--10},
year={2022},
publisher={Springer}
}
Introdución
Las Redes Neuronales Covolucionales (CNNs) son modelos computacionales que requieren una cantidad elevada de cálculos, tanto en la etapa de entrenamiento como en la etapa de inferencia. Por esta razón, una de las técnicas más utilizadas para implementar las CNNs es reordenar las operaciones desde un punto de vista computacional como una multiplicación de matrices(Gemm). En este proyecto se realiza una implementación de la Gemm), enfocado a la convolución de Redes Neuronales, en uno de los cores RISC-V del procesador GAP8 de GreenWaves.
Para esta implementación, nuestro enfoque aprovecha los algoritmos de BLIS (Basic Linear Algebra Instantiation Software) para desarrollar una implementación que :
- Reorganiza el algoritmo Gemm adaptando su micro-kernel para explotar el producto escalar soportado por el hardware en el GAP8.
- Orquesta explícitamente las transferencias de datos a través de la jerarquía de memorias scratchpad mediante DMA (acceso directo a memoria).
- Opera con aritmética de enteros(int8).
Importancia de la Multiplicación de matrices en Machine Learning
La multiplicación general de matrices conocida en Inglés como GEMM(General Matrix Multiplication), es una de las operaciones fundamentales que se presentan mas a menudo en las redes neuronales, es decir dentro de algunas de las capas mas conocidas encontramos que su funcionamiento esta basado en operaciones del tipo GEMM, AXPY o un DOT.
Por enumerar algunas de las capas que contienen la GEMM tendriamos :
- Fully-connected.
- Recurrent-layers:
- RNNs (Redes Neuronales Recursivas)
- LSTMs(Long short-Term Memory)
- GRUs(Gate recurrent Units) y por supuesto las conocidas Redes convolucionales .
Como vemos casi todas :P. Si bien es cierto la multiplicación de matrices abarca un gran numero de algoritmos, iniciando por el algoritmo nativo(naive), hasta el presentado por Alman J, Williams en 2020. Lo que se ha intentado en este articulo es comprender los algoritmos desde un punto computacional, y el rendimiento que este tiene al momento de ser implementado en diferentes arquitecturas.
Definimos que es la GEMM.
Como mencionamos antes, La operación GEMM no es mas que el producto general de matrices, este se define matemáticamente como :
$C = \alpha A \times B + \beta C$
Donde :
- A y B : son matrices de entrada
- alpha y beta : Como estradas escalares
- C : la matriz donde vamos a escribir los resultados.
Si ya nos estamos preguntando para que sirve alpha y beta, estas se incluyen en la mayoría de frameworks de algebra lineal y son dos entradas que nos permiten escalar los coeficientes de las matrices, alpha escala el producto de A*B y beta escala la matrix de salida.
Modelo computacional
Si damos un salto desde la parte teórica y abordamos los conceptos desde un punto computacional, debemos tomar en cuenta que estos conceptos llevan desarrollándose desde muchos años atrás, existiendo una gran cantidad de Librerías especializadas para este tipo de operaciones que son fundamentales en las ciencias de la computacion. Algunas de las Librerías de Algebra lineal mas utilizadas son OpenBLAS(Basic Linear Algebra Subprogramas), intel MKL(Math Kernel Library) y CuBLAS de NVIDIA. En su mayoría estas librerías utilizan las siguientes convenciones :
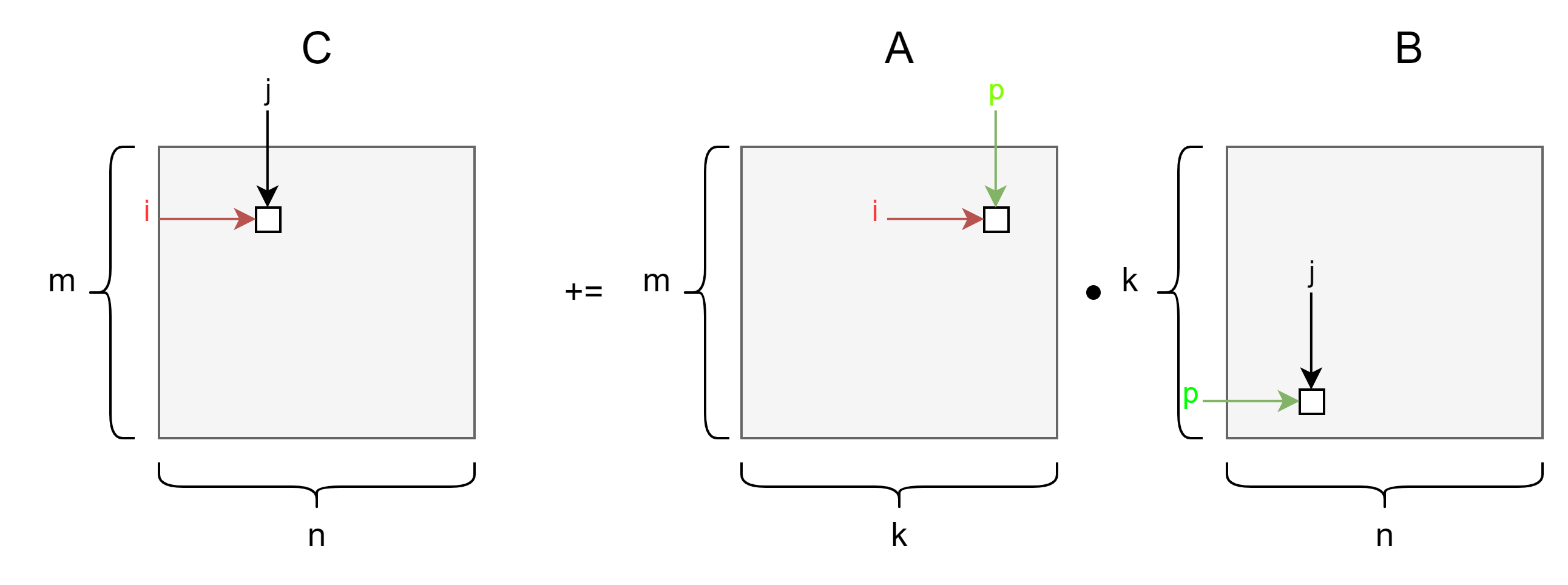
- $ A(m \times k) $ : m : filas, k: columnas.
- $ B(k \times n) $ : k : filas, n: columnas.
- $ C(m \times n) $ : m : filas, n: columnas.